5.1 分子动力学1
从头算分子动力学(ab initio molecular dYnamics, AIMD),又称为第一性原理分子动力学,为研究电子与原子核相互耦合系统的力学进动过程的理论方法。AIMD是在早期经验力场分子动力学基础上发展起来的理论方法。经验力场分子动力学中,针对原子核之间相互作用,均采用经验性的力场,这种力场往往是对相互作用,基于这些相互作用势场好处是计算量小,能够模拟的体系较大,模拟时长也比较长,统计数据也较多。
最初的AIMD为理想的Born-Oppenheimer分子动力学(BOMD),该理论将原子核-电子耦合体系的运动问题拆分为电子结构和分子动力学两部分,用密度泛函(DFT)等方法对特定原子核构型下的电子结构进行计算,得到K-S轨道及能量,在此基础上得到理想B-O势能面上原子核感受的势能和力,进而用经典力学来考察原子核在Born-Oppenheimer势能面上的运动。
为解决理想的BOMD所遇到计算瓶颈的问题,Reberto Car和Michele Parrinello于1985年提出了一种近似的BOMD方法- Car-Parrinello MD(简称CPMD)(Car, R., & Parrinello, M,1985)。该方法首次使用了一个扩展的Lagrangian量来描述电子-原子核耦合体系的动力学问题,Lagrangian量引入了虚拟电子质量u,基于这个Lagrangian量可给出运动方程,通过原子核的经典运动来近似更新电子波函数,而不再需要每一步通过矩阵对角化对电子结构进行SCF计算,简化了电子结构计算,大幅降低了计算成本,使得AIMD在技术上首次具备了可操作性,开创了近几十年AIMD模拟的时代。
第一性原理分子动力学(AIMD)结果分析
与经典分子动力学不同,第一性原理分子动力学不需要提供力场参数,只需要提供原子初始结构,就能根据电子波函数正交化产生的虚拟力,求解牛顿运动方程。在运行优化任务时,VASP生成的XDATCAR记录的是优化步骤的离子构型;在运行AIMD任务时,记录的就是运动轨迹。而现阶段读取XDATCAR轨迹分析性质的后处理软件并不多,能读取的兼容性也并不好。__VASPKIT0.72版本之后支持了将XDATCAR转换成通用的多帧PDB文件的功能(504)以便可视化并进行后处理分析__。但是并没有提供后处理分析接口,因此我们开发了一个Python脚本XDATCAR_toolkit.py,除了实现了选择一定范围内的帧数转换成PDB文件的功能,还可以提取分子动力学模拟过程中的能量,温度并做出变化趋势图。这对判断动力学是否平衡很有帮助。另外本脚本预留了接口,可以调用读取每一帧的晶格信息和原子坐标,以便进行后续扩展编程。此脚本需要安装了numpy包的python环境,以及matplotlib包以便于画图。
在得到通用轨迹PDB文件后,就可以利用现用的分子动力学后处理软件进行处理分析,比如VMD,MDtraj,MD Analysis, Pymol等。__本教程将演示通过VMD和MD Analysis软件包分析RDF(径向分布函数)和RMSD(均方根偏差)__,前者可以用来分析结构性质,后者对判断结构是否稳定以及模拟是否平衡很有帮助。
将XDATCAR转换成PDB文件
以VASP官网中单个水分子的AIMD模拟为例。模拟的输入文件如下,模拟的步长是0.5fs,模拟步数1000步,模拟时间500fs。脚本和测试例子可以在Github仓库(https://github.com/tamaswells/VASP_script/tree/master/XDATCAR_tookit)下载。
图1. 模拟的盒子
INCAR
1 | PREC = Normal ! standard precision |
POSCAR
1 | H2O _2 |
KPOINTS
1 | Gamma-point only |
模拟完成后将XDATCAR_toolkit.py上传到文件夹中(或者置于环境变量的路径文件夹中并赋予可执行权限即可直接调用命令XDATCAR_toolkit.py运行脚本),在shell环境中运行以下命令:
python XDATCAR_toolkit.py -p -t 0.5 --pbc
即可将XDATCAR的全部帧也就是0~499.5fs的轨迹转化成PDB格式。其中-p用于开启PDB转换功能,-t 0.5用于指定时间步为0.5fs,–pbc用于获取基于第一帧演变的连续轨迹。
1 | Now reading vasp MD energies and temperature. |
运行完成后,将会在文件夹内生成Temperature.dat,Energy.dat,ENERGY.png和XDATCAR.pdb四个文件,前面两个分别为温度和能量随着模拟时间的的变化数据,第三个是使用matplotlib绘制的趋势图(如下图),最后一个是转换得到的轨迹PDB文件,可以用于可视化轨迹,亦可用于后处理分析。
-b参数用于指定转换从哪一帧开始,-e参数用于指定转换到哪一帧结束。经刘锦程博士建议,增加一个–pbc的选项,用于处理周期性获取连续的轨迹。当分子穿过盒子边界时,记录真实的位置坐标(尽管它出了边界)而不是从盒子另一边穿入的ghost原子的坐标。这对于分析与时间相关性的量(比如RMSD)很有帮助。所谓连续指的是后面的轨迹都是从第一帧演变得到的真实坐标,但是并不能保证第一帧的分子是完整的,由于周期性的缘故,第一帧内摆放的分子可能分处于盒子两侧。李继存老师有篇博文(http://jerkwin.github.io/2016/05/31/GROMACS%E8%BD%A8%E8%BF%B9%E5%91%A8%E6%9C%9F%E6%80%A7%E8%BE%B9%E7%95%8C%E6%9D%A1%E4%BB%B6%E7%9A%84%E5%A4%84%E7%90%86/)讲的很明白,可以参考。如果发现第一帧内分子不完整,可以通过添加`-i 1参数将分子向第一个原子靠近平移以获得完整的分子。如果发现不理想,可以通过调整-i`的参数获得完整的分子。
图2. 温度和系统能量的变化趋势图
RDF径向分布函数分析
得到PDB文件后,可以使用VMD,MD Analysis等分子动力学后处理软件进行分析。
使用VMD分析工具分析
打开VMD,将PDB文件拖入显示窗口,在主菜单VMD Main中选择
Extensions-Analysis-Radial Pair Distribution Function g(r),选择分析H(type H)在O(type O)周围的概率分布。值得注意的是分析RDF时,横坐标也就是max r不能超过盒子最小边长的一半,也就是得满足最小映像约定。如图4所示,在计算RDF时,如果max r的取值大于盒子最小边长的一半,就有可能重复算到一个粒子和它的映像粒子,这使得程序的周期性判断失准。将生成的dat文件的第一列和第二列作图即可得到RDF图。
图3. VMD中计算RDF
图4. 最小映像约定示意图
使用 MD Analysis分析 RDF
MD Analysis是一个成熟的分子动力学后处理软件,使用Python编写,开源。其教程不仅步骤详细还会给出背景理论知识。可以通过conda或者pip工具在线安装。
1 | conda config --add channels conda-forge |
RDF分析的介绍和使用方法在网页(https://www.mdanalysis.org/docs/documentation_pages/analysis/rdf.html#radial-distribution-functions-mdanalysis-analysis-rdf)上查看。使用以下的脚本得到在O原子周围找到H原子的概率,并调用`matplotlib`绘制RDF图。在1.0 Å
处出现一个尖峰,也就是对应了O-H键的平衡键长(0.96$Å$)。
1 | import MDAnalysis |
图5. RDF_O_H
RMSD均方根偏差分析
VMD分析RMSD
确保使用了-pbc参数以获取连续的轨迹,将生成的XDATCAR.pdb文件拖入显示窗口。如图6右所示,第一帧内水的三个原子不在同一个镜像内,分子不完整。在进行RMSD分析时,尽管轨迹是连续的,但是在对齐分子时就会出现问题。因此在本例中需要选择第一个原子作为中心将分子平移完整,在图6左中,分子已经在同一个镜像中了。
python XDATCAR_toolkit.py -p -t 0.5 --pbc -i 1
图6. 完整和不完整的水分子
将重新生成的PDB文件拖入显示窗口,在主菜单VMD Main中选择Extensions-Analysis-Analysis-RMSD Trajectory Tool,在计算RMSD前必须先做Align(对齐),这会使得每一帧结构进行平移、旋转来与参考帧的结构尽可能贴近,从而使得RMSD最小化。刘锦程提到研究生物法分子的RMSD时需要对齐操作,而研究小分子时不需要对齐分子。
图7. VMD中计算RMSD
把左上角文本框里的默认的Protein改成all(代表所有原子都纳入考虑),然后把noh复选框的勾去掉(否则将忽略氢原子)。然后点右上角的ALIGN按钮,此时所有帧的结构就已经对齐了。本例中演示以模拟的第一帧为参考,分析氧原子位置的均方根偏差。因此在Reference mol那里选top作为参考结构,左上角文本框由all改为type O(代表计算O原子的RMSD),然后勾上Plot复选框,最后点击RMSD按钮即可得到O原子的RMSD图。在File菜单栏可以选择导出dat数据。
图8. VMD中未对齐轨迹计算的RMSD
图9. VMD中对齐了轨迹后计算的RMSD
使用 MD Analysis分析 RMSD
RMSD分析的介绍和使用方法在网页(https://www.mdanalysis.org/docs/documentation_pages/analysis/rms.html?highlight=average)上查看。
使用以下的脚本可以分别得到所有原子,氢原子,氧原子的RMSD,并调用matplotlib绘制RMSD图。网页中有一段话(Note If you use trajectory data from simulations performed under periodic boundary conditions then you must make your molecules whole before performing RMSD calculations so that the centers of mass of the selected and reference structure are properly superimposed.)也就是在计算RMSD的时候选择的分子必须是完整的,不能分处于盒子的两边。这与我们之前的描述是一致的。MD Analysis默认对齐了分子。
使用以下脚本可以绘制对齐了轨迹后所有原子,氧原子和氢原子的RMSD。
1 | import MDAnalysis |
应用python工具pymatgen,
可以直接得到MSD,diffusion,donductivity。
得到XDATCAR后,需要首先配置pymatgen。
需要用到conda命令,windows:可以安装anaconda3,通过spyder启动。
进入anaconda prompt中启动中断,配置conda environment:
1 | conda create –name my_pymatgen python |
linux环境下一个比较好的选择是安装miniconda3
wget https://repo.anaconda.com/minico … -Windows-x86_64.exe
bash Miniconda3-latest-linux-x86_64.sh
如果原来在bashrc中配置了anaconda,则注释掉,重启terminal。
与windows下相同,需要设置一个pymatgen环境。
1 | conda create –name my_pymatgen |
在my_pymatgen环境下安装 pymatgen:
conda install --channel conda-forge pymatgen
安装好之后运行建立如下test.py脚本, 可以得到结果:
1 | import os |
在1.dat中是msd,conductivity和diffusivity会直接输出在result.dat中,模拟石墨烯表面Li的MD(excessive state)结果diffusivity为2*10-7 cm^2/S,我觉得算出diffusivity后自己求conductivity比较好,请问应该怎么求?与文件对比,基本吻合(J. Phys. Chem. Lett. 2010, 1, 1176–1180;https://pubs.acs.org/doi/10.1021/jp910134u)。
其它不对的地方,欢迎批评指正。
参考:
https://pymatgen.org/installation.html
https://www.bigbrosci.com/2020/09/08/A18/
VTST的脚本里有一个xdat2xyz.pl,可以直接把XDATCAR转化成movie.xyz文件。xdatcar可以通过ase转换成ms的xtd,也可以转ext-xyz,理论上支持xyz格式的程序也能打开。ase convert xdatcar xxx.xtd(注意会生成隐藏文件xxx.arc,如果要移动xtd,应该要使两个文件在相同的目录)。
事实上,有xtd格式的话,如果你有MS的版权,有些针对xtd格式的分析其实可以直接在MS里面做。arc文件跟着xtd一块拷贝到相同目录。
离子的电导率
Pymatgen 是 python materials genomics 的缩写,它是一款基于 python 的、开源的、强大的材料分析软件(https://pymatgen.org/)。
Pymatgen 包含一系列能够表示元素(Element)、位点(Site)、分子(Molecule)、和结构(Structure)的类(Class)。它具有为很多计算软件提供前处理和后处理的能力。这些计算软件包括VASP,ABINIT,exciting,FEFF,QCHEM,LAMMPS,ADF,AIIDA,ASE,Gaussian,Lobster,Phonopy,Shengbte,Pwscf,和Zeo++等等。它能实现科研狗的众多后处理需求,包括生成相图(Phase diagram)和布拜图(Pourbaix diagrams),分析态密度和能带等等。
Pymatgen 还提供了很多数据库(Materials Project REST API,Crystallography Open Database,and other external data sources)的接口,方便大家从数据库中查询结构和其他数据。
以下是Pymatgen官网提供的后处理的例子:
Top: (left) Phase and (right) Pourbaix diagram from the Materials API. Bottom left: Calculated bandstructure plot using pymatgen’s parsing and plotting utilities. Bottom right: Arrhenius plot using pymatgen’s DiffusionAnalyzer.
本文就介绍一下如何使用 Pymatgen 的 DiffusionAnalyzer 类去计算锂离子固态电解质中锂离子电导率。
计算离子电导率的理论与公式
目前,比较准确的计算离子电导率的方法是先用NVT系综第一性原理分子动力学(AIMD,ab initio molecular dynamics)模拟材料中离子在不同温度下的运动,然后计算出离子的平均(average)均方位移(MSD,mean square displacement),再计算出自扩散系数(D
,self-diffusion coefficient),最后求得离子在某温度下的电导率(
,conductivity)。
如何进行AIMD计算
AIMD计算通常非常耗时,所以,为了减少计算成本,我们可以适当放宽计算精度。如果用 VASP 进行计算,具体的,大家可以
采用较小的截断能。氧化物用 400 eV,硫化物用 280 eV,硒化物用 270 eV
采用Gamma点作为K点设置,并使用gam版本的 VASP 进行计算
采用单胞计算,如果材料的单胞包含比较多的原子
采用合适的步长,比如2 fs,即 POTIM = 2
后处理的基本公式
一旦AIMD计算完成,大家就可以着手计算离子电导率了。本文首先先介绍以下计算过程中使用的公式,方便有兴趣的同学自己开发脚本。
平均均方位移(average MSD)可以通过以下公式计算:
是第
个离子在
时刻的位移。
自扩散系数(
)可以通过以下公式计算:
是离子在材料中的扩散维度(一般地,
),
是离子扩散的时间。
最后,离子电导率(
)可以这样计算:
是材料中的离子密度,
是元电荷,
是离子的价态,
是玻尔兹曼常数,
是温度。
电导率计算的例子
现在我们通过一个 Li_Sn_S 材料的例子来详细了解一下整个计算和处理的过程。该材料的结构显示如下:
本例中采用单胞做计算,INCAR 设置如下:
[test@ln0%tianhe2 li_sn_s]$ vi INCAR
1 | ISTART = 0 |
AIMD 计算结束之后会得到 XDATCAR 文件。很多时候,由于超算的时间限制,一个完整的AIMD计算需要提交两三次,从而产生两三个 XDATCAR 文件,这时,我们只要把它们按顺序通过 cat 命令合并在一起就行。例如我们有三个 XDATCAR 文件,分别命名成 XDATCAR01,XDATCAR02,和 XDATCAR03。
[test@ln0%tianhe2 li_sn_s]$ cat XDATCAR01 XDATCAR02 XDATCAR03 > XDATCAR
新得到的XDATCAR文件,注意删掉重复的与晶格信息相关的行,一般续算的次数也不多,在使用上面命令的时候,手动把XDATCAR02, XDATCAR03 中的删除即可。
Pymatgen 大显身手
安装pymatgen
首先让我们安装 pyamtgen,推荐大家参考官网,使用 anaconda 安装,否则会出现问题。安装好了anaconda之后,不管是 linux 还是 windows, 安装 pyamtgen 的指令是一样的。下面以吕梁天河超算为例:
[test@ln0%tianhe2 li_sn_s]$ conda install –channel conda-forge pymatgen
安装完成后,我们可以试着运行 python,导入 Pyamtgen 模块,如果像下面一样没有出错,就是安装成功了。
1 | [test@ln0%tianhe2 li_sn_s]$ python |
查看 DiffusionAnalyzer 的类
大家可以通过官方文档(https://pymatgen.org/pymatgen.analysis.diffusion_analyzer.html)查看接下来要使用的类,熟悉一下代码的用法。
1 | class DiffusionAnalyzer(MSONable): |
这段代码显示,运行这个类需要一系列的输入信息,包括材料结构(structure),位移(displacements),要研究的离子(specie),温度(temperature)等等。
但是这个类提供了很多方法让大家可以通过读取 XDATCAR 或者 vasprun 文件的方式来实例化,例如
1 | @classmethod |
好了,废话不多说,直接上代码,开始进行后处理。
代码示例
新建一个文件,名字为li_conductivity.py
‘’’
分析AIMD结果,计算MSD 和 conductivity
‘’’
1 | import os |
在终端运行该文件
1 | [test@ln0%tianhe2 li_sn_s]$ python li_conductivity.py |
一段时间后就会得到MSD图像和离子电导率
1 | [test@ln0%tianhe2 li_sn_s]$ vi result.dat |
可见,该材料在 900K 时的锂离子电导率为 884.05 mS/cm。
例子下载:
链接:https://pan.baidu.com/s/1WGzOVJBoe6Ym8mvR1uWanA
提取码:jhc5
思考
简短几行代码就可以计算出离子电导率,那么如何得出材料在300K下的电导率呢?
如何计算离子在材料中的迁移势垒?
如何可视化离子在材料中的扩散路径?
如何使用 Pymatgen 可视化离子的迁移概率密度。
先举个例子,
在“Design principles for solid-state lithium superionic conductors”一文中(Wang et al., Nature Materials 2015, 14 , 1026–1031. ),作者用Ab Initio Molecular Dynamic (AIMD)计算了Li 离子在Li$\mathrm{_1}\mathrm{_2},
\mathrm{_7}
\mathrm{_3}
\mathrm{_1}$$\mathrm{_1},
\mathrm{_2},和
\mathrm{_4}
\mathrm{_4}$ 四种材料中的迁移概率密度(Probability Density),结果如下图所示:
从图中可以看出Li离子在图a所示材料中主要沿c轴方向的通道迁移,而且由于这个通道连通得比较好,Li离子的迁移势垒会比较低(0.220.25 eV)。0.19 eV)。
Li离子在图b所示的材料的迁移路径形成了一个三维网格,而且由于这个概率密度比图b中的概率密度分布得更加均匀,Li离子的迁移势垒更低(0.18
图b所示的材料就完全不行了,因为Li离子的概率密度仅分布在特定的位点附近,说明离子不能有效地移动。
Li离子在图d所示材料中也存在迁移局域化的行为。
作者总结说 “A general principle for the design of Li-ion conductors with low activation energy can be distilled from the above findings: all of the sites within the diffusion network should be energetically close to equivalent, with large channels connecting them.”
那么我们如何在自己的计算中画出这样的图呢?Pymatgen 举手说,它可以帮忙!
但是在开始之前,我们要安装Pymatgen的插件:Pymatgen-diffusion(https://github.com/materialsvirtuallab/pymatgen-diffusion)。
安装 Pymatgen-diffusion
推荐大家使用最新版的Anaconda安装Pymatgen及其插件。点击上面的链接,进入官网后,点击最新版本链接,
我们可以下载.zip文件,
下载完成后,大家可以解压这个文件,得到 pymatgen-diffusion-2019.8.18文件夹。
我们把其中的 pymatgen_diffusion 文件夹放到 Anaconda的site-packages文件夹下,路径是 Windows 系统:……\Anaconda\Lib\site-packages;Linux系统:……/anaconda3/lib/pythonx.x/site-packages,就算安装好了。
接下来我们可以启动python,导入这个模块,如果不报错就没有问题了。
1 | [test@ln0%tianhe2 li_sn_s]$ python |
学习用法
我们可以在其github网站上通过例子学习这个模块的用法。
点击打开 probbility_analysis.ipynb 文件。
其内容如下(有所删减):如果不想看的话可直接查看 开始作图 部分
1 | from pymatgen.analysis.diffusion_analyzer import DiffusionAnalyzer |
开始作图
代码(test.py)如下:
1 | from pymatgen_diffusion.aimd.pathway import ProbabilityDensityAnalysis |
此处理过程大概耗时8分钟,因机器而异。
在VESTA中可视化
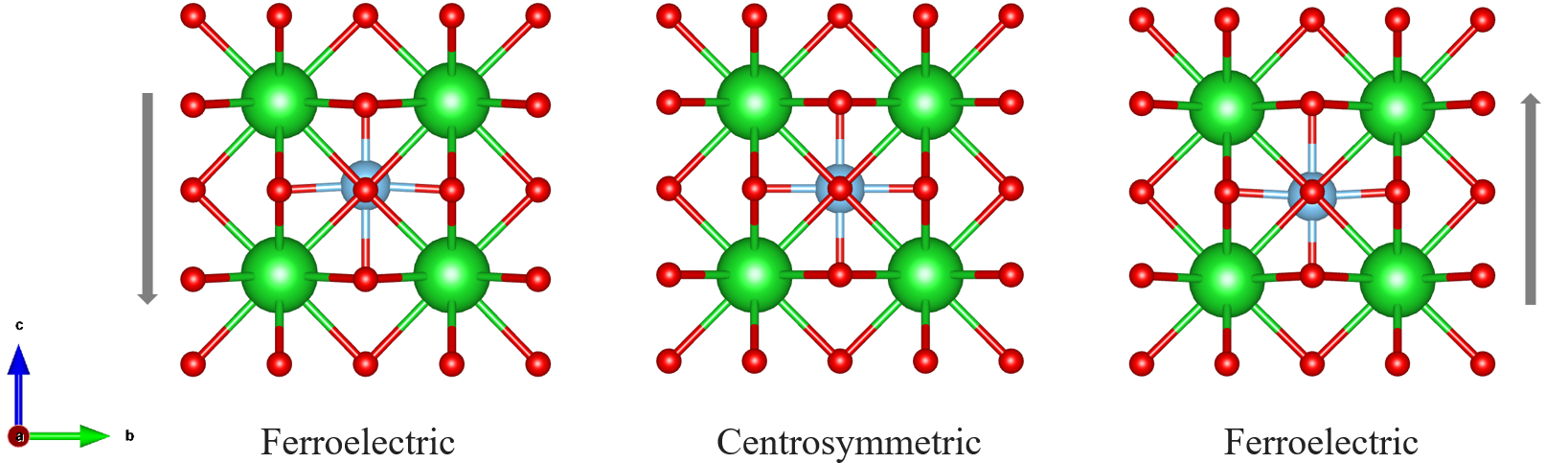 ,属于四方晶系。
,属于四方晶系。